- Understanding options pricing
- What’s an in-the-money option?
- What’s an out-of-the-money option?
- What’s an at-the-money option?
- The Greeks
- What is delta?
- What is vega?
- What is theta?
- What is gamma?
- What is rho?
Understanding options pricing
Like any financial instrument, the price of an option is ultimately determined by the markets – the constantly changing supply and demand (bids and offers) for that particular contract. Since options contracts can offer substantial leverage, they tend to experience price swings that may seem unpredictable at first glance.
Learn more about what an option is and how to trade it
Traders throughout the world use a common framework for evaluating options prices based on the original Black-Scholes pricing formula developed in 1973.
Put simply, the model creates a small set of variables, known as ‘the Greeks’, that are extremely valuable to options traders. It’s not necessary to become an expert in the calculus that drives the Nobel Prize-winning formula, as pricing is automatic on trading platforms like ours, but it is useful to understand the concepts that make up the calculations.
Before we dive into the Greeks, let’s look at some other terms you’ll need to know.
What’s an in-the-money option?
An in-the-money option is an option in which the underlying market has already moved beyond the strike price so that if it settled today, it would have some value. This amount is called the intrinsic value of the option.
For example, if the S&P 500 is trading at 3750 and you are long the Daily 3700 Call, you are in the money. The option already has an intrinsic value of 50 (the difference between the strike price and the underlying market).
What’s an out-of-the-money option?
An out-of-the-money option is an option whose underlying market hasn’t moved beyond the strike price, so it has no intrinsic value. If the option expired today, it would be worth zero.
For example, if the S&P 500 is trading at 3750 and you are long the Daily 4000 Call, you are currently out of the money.
However, if the option expires sometime in the future it will still be worth something today even though its intrinsic value is zero. This is because an option also has time value – known as extrinsic value – based on the possibility that it could eventually land in the money before it expires.
What’s an at-the-money option?
An at-the-money option is one with a strike price that sits right at or near the underlying market. For example, if the S&P 500 is trading 3750 and you are long the Daily 3750 Call, you are at the money.
At-the-money options have no intrinsic value but they’re so close to being in the money that they have earned their own identity. These are often some of the most actively traded options in any market.
The Greeks
There are five headline ‘Greeks’ in options trading: delta, vega, theta, gamma and rho.
What is delta?
Delta is a way to measure the relationship between an option and the underlying market. It’s the most commonly referenced option variable because it gives you a baseline for the expected changes in the value of an option contract that you might buy or sell.
Delta is often called ‘the fractional Greek’ because it views the option as being a fraction of the underlying market. Delta assigns a value between 0% and 100% to every options contract that gives you an idea of the option’s relationship to price movement in the underlying market. So, an option with a delta of 25% would be expected to increase in value by $2.50 if the underlying market increases by $10.
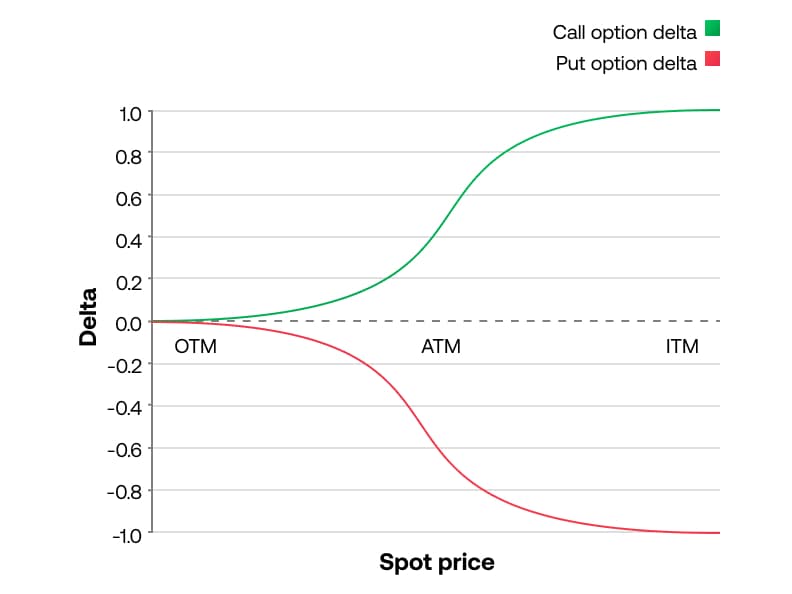
Looking at the delta can tell us a lot about the characteristics of a potential trade. Low-delta options (less than 10%) are typically very far out of the money and would need a large price move to increase in value. An option with a 95% delta, on the other hand, is very deep in the money and therefore behaves almost the same as a position in the underlying market.
At-the-money options usually have a delta of 50%. This means that if the value of the underlying market goes up by $10, the 50-delta call option would increase in value by around $5.
Think of a position using another instrument, such as a CFD, as a 100-delta position because it moves one for one with the underlying.
Delta polarity – whether the value is positive or negative – is essential to options strategies. Here are some general rules of thumb for delta polarity:
- Positive delta (bullish positions): you’d be long on the underlying market using long calls or short puts
- Negative delta (bearish positions): you’d be short on the underlying market using short calls or long puts
Ready to start options trading? Open an account today or practise trading options first in a risk-free demo account.
What is vega?
Vega is the Greek that accounts for implied volatility, which is the annual expected range of the underlying market. It’s simply a way to estimate the impact of changes in the option’s implied volatility to changes in the option’s price.
So, an option that is currently worth $50 might have a vega value of $12. This means that each 1% increase in implied volatility will increase the option’s value by $12, regardless of whether or not the underlying market moves at all.
Underlying markets that have a very volatile trading range would have a higher implied volatility, which translates into a higher option prices. For example, AUD/USD (Aussie Dollar) is considered a relatively stable FX pair, whereas a stock like Tesla (TSLA) often moves quite a bit during any given time frame. So, an out-of-the-money option in TSLA is going to be worth a lot more than a comparable out-of-the-money option in AUD/USD.
It’s important to note that implied volatility is a theoretical, forward-looking value. After all, nobody really knows what the range of TSLA is going to be for the next year.
Implied volatility is calculated by taking the market price of an option and then reverse-engineering the ‘implied’ volatility number in the Black-Scholes model. The actual, or historic, volatility does not factor into the price of an option.
For example, if you look up the current implied volatility of TSLA options and you get a value of 50%, you might then look at a chart and notice that TSLA shares have moved over a 300% range over the past year. But this makes no difference – if the implied volatility is 50% then you know that the options market is expecting a range of 50% over the next year.
Vega enables you to make judgement calls about when is going to be a good time to buy options, and when you’d be paying a very big premium and would therefore need a very large move in the underlying market to get the payoff you’d like.
For example, you might want to buy S&P 500 Put options during earnings season in the expectation that key companies will miss their earnings targets and the market will go down fast. You see that those put options are trading at an implied volatility of 40%, even though the usual implied volatility for the S&P 500 is below 20%. This tells you that the options are considerably more expensive right now.

What is theta?
Theta is how we measure the daily ‘time decay’, or the amount by which the option loses a little bit of value each day. Options have an expiration date, so each minute that goes by reduces the probability that the option will have a high intrinsic value at settlement. Options that expire within a week have the most theta.
For daily options traders, theta has a much smaller timeframe over which to work. However, you’ll still need to be aware of it depending on which time of day you’re entering a position.
Let’s look at an example. You buy an out-of-the-money option today for $3 and it has three hours remaining until expiration. The underlying market doesn’t move at all (no delta impact) and the implied volatility doesn’t change (no vega impact), but that option is still likely to lose value because of the time decay.
Think of it this way: an out-of-the-money option has an intrinsic value of zero. If the underlying market doesn’t move, it will expire worthless. So, as time keeps ticking, the value of the option slowly grinds lower.
Theta can work for or against you, depending on whether you have bought or sold the option. If you are an option seller, theta is likely your favourite Greek because it continuously works in your favour, slowly but surely. Those who favour buying options often view theta as a cost of doing business – it’s the amount you steadily lose while you stay in the game trying to profit on delta and vega movement.
What is gamma?
Gamma is probably the least understood of the Greeks. By definition, it is a measure of the rate at which the delta of the option is changing as the underlying market moves. Think of it as the delta of the delta – the rate of change of the rate of change.
To visualise how gamma works, consider a 5% delta call option, with a strike price of 140 and an underlying market currently at 100. We know that if the underlying market moves up to 101, the value of the 140 Call option will increase by $0.05 (since it has a 5% delta on a $1 underlying move).
Now imagine that the market has moved all the way up to 140, so that the option is now at the money and therefore has a delta of 50%, at this level, a $1 underlying move will result in a $0.50 change in the same option’s price – representing a far larger exposure to the market.
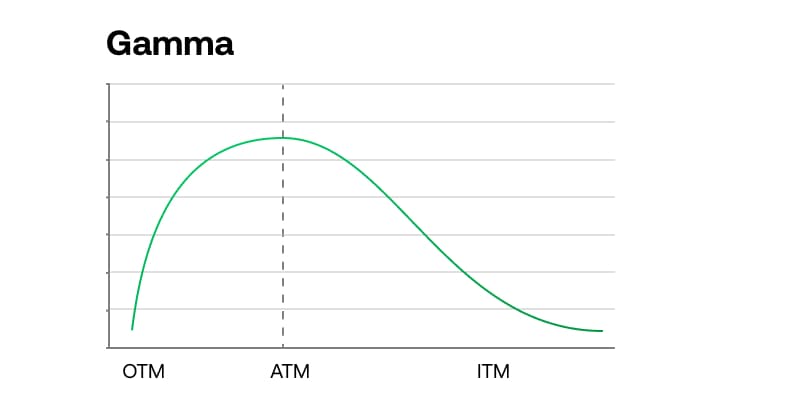
So, while the delta can help us predict the change in value across a small underlying price move, we really need to understand that the gamma is working to continuously change the delta during any given move.
Gamma helps us understand how options come alive in a fast-moving market. It makes it difficult to continuously hedge a short option position because it forces you to keep buying at higher prices (or selling at lower prices) to keep up with the changing delta. Gamma shows us the effects of compounding leverage in options, which can be extremely beneficial when you are long options, and very costly when you are short.
What is rho?
Rho is the measure of interest-rate sensitivity in options. It’s often called ‘the boring Greek’ because it is downright useless these days. That’s thanks to decades of central bank easing, which have left interest rates stuck at levels in which there is no meaningful impact on options pricing.
However, that could change in the future so it’s something to be aware of. There is an opportunity cost to own an expensive option for a long period of time if it could have been earning interest in a bank account. Also, it’s worth noting that just because interest rates are near zero in Europe, Japan, and most English-speaking countries, there are many nations with well-established financial trading markets where rates are still quite high. All else being equal, higher interest rates reduce the value of most options.
How to trade options
You can trade options via CFDs in just a few quick steps:
- Learn how to trade CFDs
- Create an account with City Index
- Find the daily options market you want to trade
- Choose between a call or put option
- Open your position
- Monitor and close your trade
Find out how CFDs work and the benefits of trading derivatives
Get started trading on live markets, or practise trading first in a risk-free demo account
Browse the ‘Options’ section in our award-winning platform or use the ‘search’ feature to quickly find your market
Decide whether you think the market will rise or fall, and choose a strike price to ‘buy’ or ‘sell’ at
Enter your quantity and price tolerance and select ‘place trade’
Use analysis to stay up to date with any price movements and identify an exit point for your position
FAQs
What is an option’s exercise price?
An option’s exercise price is another word for the strike price, the level at which the contract can be executed. Until the underlying market has reached or passed this level, the option has no intrinsic value and is out of the money.
Learn more about what options are and how they work.
How are stock options priced?
Stock options are priced using the underlying share price – most share options represent 100 of the underlying stock. As the price of a stock rises, the price of a call option on the shares would rise, while the price of a put option on the shares would fall – and vice versa for when the stock price falls. As with any option, there are other factors that go into pricing, such as intrinsic value, time to expiry and volatility.









